Определение 1

Случайна променлива $X$ се нарича дискретна (прекъсната), ако наборът от нейните стойности е безкраен или краен, но изброим.

С други думи, количеството се нарича дискретно, ако стойностите му могат да бъдат номерирани.

Случайна променлива може да бъде описана с помощта на закона за разпределение.

Законът за разпределение на дискретна случайна променлива $X$ може да бъде зададен под формата на таблица, чийто първи ред показва всички възможни стойности на случайната променлива във възходящ ред, а вторият ред съдържа съответните вероятности за тях стойности:

Снимка 1.

където $р1+ р2+ ... + рn = 1$.

Тази маса е близо до разпределението на дискретна случайна променлива.

Ако наборът от възможни стойности на случайна променлива е безкраен, тогава серията $р1+ р2+ ... + рn+ ...$ се сближава и нейната сума ще бъде равна на $1$.

Законът за разпределение на дискретна случайна величина $X$ може да бъде представен графично, за което се построява начупена линия в координатната система (правоъгълна), която последователно свързва точки с координати $(xi;pi), i=1,2, ... n$. Линията, която получихме, се нарича разпределителен полигон.

Фигура 2.

Законът за разпределение на дискретна случайна променлива $X$ може също да бъде представен аналитично (като се използва формулата):

$P(X=xi)= \varphi (xi),i =1,2,3 ... n$.

Операции върху дискретни вероятности

При решаването на много проблеми в теорията на вероятностите е необходимо да се извършат операции за умножаване на дискретна случайна променлива с константа, добавяйки две случайни променливи, умножавайки ги, издигайки ги на степени. В тези случаи е необходимо да се спазват следните правила за случайни дискретни величини:

Определение 3

Умножениена дискретна случайна променлива $X$ по константа $K$ е дискретна случайна променлива $Y=KX,$, която се определя от равенствата: $y_i=Kx_i,\ \ p\left(y_i\right)=p\ ляво(x_i\дясно)= p_i,\ \ i=\overline(1,\ n).$

Определение 4

Извикват се две случайни променливи $x$ и $y$ независима, ако законът за разпределение на едно от тях не зависи от това какви възможни стойности е придобило второто количество.

Определение 5

Количестводве независими дискретни случайни променливи $X$ и $Y$ се наричат ​​случайна променлива $Z=X+Y,$ се определя от равенствата: $z_(ij)=x_i+y_j$, $P\left(z_(ij )\right)= P\left(x_i\right)P\left(y_j\right)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$ , $P\left (x_i\right)=p_i$, $P\left(y_j\right)=p"_j$.

Определение 6

Умножениедве независими дискретни случайни променливи $X$ и $Y$ се наричат ​​случайна променлива $Z=XY,$ се определя от равенствата: $z_(ij)=x_iy_j$, $P\left(z_(ij)\right) =P\left( x_i\right)P\left(y_j\right)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$, $P\ left(x_i\right )=p_i$, $P\left(y_j\right)=p"_j$.

Нека вземем предвид, че някои продукти $x_(i\ \ \ \ \ )y_j$ могат да бъдат равни помежду си. В този случай вероятността за добавяне на продукта е равна на сумата от съответните вероятности.

Например, ако $x_2\ \ y_3=x_5\ \ y_7,\ $тогава вероятността $x_2y_3$ (или същото $x_5y_7$) ще бъде равна на $p_2\cdot p"_3+p_5\cdot p"_7 .$

Горното важи и за сумата. Ако $x_1+\ y_2=x_4+\ \ y_6,$ тогава вероятността $x_1+\ y_2$ (или същото $x_4+\ y_6$) ще бъде равна на $p_1\cdot p"_2+p_4\cdot p"_6. $

Случайните променливи $X$ и $Y$ се определят от законите за разпределение:

Фигура 3.

Където $p_1+p_2+p_3=1,\ \ \ p"_1+p"_2=1.$ Тогава законът за разпределение на сумата $X+Y$ ще има формата

Фигура 4.

И законът за разпределение на продукта $XY$ ще има формата

Фигура 5.

Разпределителна функция

Пълно описание на случайна променлива също се дава от функцията на разпределение.

Геометрично, функцията на разпределение се обяснява като вероятността случайната променлива $X$ да приеме стойността, която е представена на числовата ос от точката, разположена вляво от точката $x$.

Цел на услугата. Онлайн калкулаторът се използва за изграждане на таблица на разпределението на случайната променлива X - броят на проведените експерименти и за изчисляване на всички характеристики на серията: математическо очакване, дисперсия и стандартно отклонение. Протоколът с решението се съставя във формат Word.

Пример 1. В урната бяло и черна топка. Топките се теглят на случаен принцип от урната, без да се връщат, докато се появи бяла топка. Веднага щом това се случи, процесът спира.
Този тип задачи са свързани с проблема за конструиране на геометрично разпределение.

Пример 2. Двама трима стрелци всеки стреля по един изстрел в целта. Вероятността първият стрелец да го уцели е , второ – . Начертайте закон за разпределение на случайната променлива X - броя на попаденията в целта.

Пример 2а. Стрелецът стреля два три четири изстрела. Вероятността за попадение със съответния изстрел е равна на , . Ако се случи първият пропуск, стрелецът не участва в следващите състезания. Начертайте закон за разпределение на случайната променлива X - броя на попаденията в целта.

Пример 3. В партията от подробности дефектни стандартни. Контролерът тегли на случаен принцип подробности. Съставете закон за разпределение на случайната променлива X - броят на дефектните добри части в извадката.
Подобна задача: В кошницата има m червени и n сини топки. K топки се теглят на случаен принцип. Начертайте закона за разпределение на DSV X - появата на сини топки.
вижте други примерни решения.

Пример 4. Вероятността събитие да се случи в един опит е равна на . Произведено тестове. Съставете закон за разпределение на случайната променлива X - броят на случванията на събитието.
Подобни задачи за този тип разпределение:
1. Съставете закон за разпределение на случайната променлива X брой попадения с четири изстрела, ако вероятността за поразяване на целта с един изстрел е 0,8.
2. Монетата се хвърля 7 пъти. Намерете математическото очакване и дисперсията на броя на появяванията на герба. Направете таблица на разпределението на Х - броя на появяванията на герба.

Пример №1. Хвърлят се три монети. Вероятността да получите герб с едно хвърляне е 0,5. Начертайте закон за разпределение на случайната променлива X - броя на изпуснатите емблеми.
Решение.
Вероятност да не е нарисуван герб: P(0) = 0,5*0,5*0,5= 0,125
P(1) = 0,5 *0,5*0,5 + 0,5*0,5 *0,5 + 0,5*0,5*0,5 = 3*0,125=0,375
P(2) = 0,5 *0,5 *0,5 + 0,5 *0,5*0,5 + 0,5*0,5 *0,5 = 3*0,125=0,375
Вероятност за получаване на три герба: P(3) = 0,5*0,5*0,5 = 0,125

Закон за разпределение на случайната променлива X:

х	0	1	2	3
П	0,125	0,375	0,375	0,125

Проверка: P = P(0) + P(1) + P(2) + P(3) = 0,125 + 0,375 + 0,375 + 0,125 = 1

Пример №2. Вероятността един стрелец да уцели целта с един изстрел за първия стрелец е 0,8, за втория стрелец – 0,85. Стрелците са произвели един изстрел в целта. Като се има предвид попадението в целта като независими събития за отделните стрелци, намерете вероятността за събитие А – точно едно попадение в целта.
Решение.
Да разгледаме събитие А - едно попадение в целта. Възможните варианти за възникване на това събитие са следните:

1. Първият стрелец попадна, вторият пропусна: P(A/H1)=p 1 *(1-p 2)=0,8*(1-0,85)=0,12
2. Първият стрелец пропусна, вторият стрелец уцели целта: P(A/H2)=(1-p 1)*p 2 =(1-0,8)*0,85=0,17
3. Първата и втората стрела уцелват целта независимо една от друга: P(A/H1H2)=p 1 *p 2 =0.8*0.85=0.68

Тогава вероятността за събитие A – точно едно попадение в целта – ще бъде равна на: P(A) = 0.12+0.17+0.68 = 0.97

При приложенията на теорията на вероятностите количествените характеристики на експеримента са от първостепенно значение. Количество, което може да бъде количествено определено и което в резултат на експеримент може да отнеме в зависимост от случая различни значения, Наречен случайна величина.

Примери за случайни променливи:

1. Колко пъти се появява четен брой точки при десет хвърляния на зара.

2. Броят на попаденията в мишената от стрелец, който стреля серия от изстрели.

3. Броят на фрагментите от експлодиращ снаряд.

Във всеки от дадените примери случайната променлива може да приема само изолирани стойности, тоест стойности, които могат да бъдат номерирани с помощта на естествена серия от числа.

Такава случайна променлива, чиито възможни стойности са отделни изолирани числа, които тази променлива приема с определени вероятности, се нарича отделен.

Броят на възможните стойности на дискретна случайна променлива може да бъде краен или безкраен (изброим).

Закон за разпределениеДискретна случайна променлива е списък от нейните възможни стойности и съответните им вероятности. Законът за разпределение на дискретна случайна променлива може да бъде определен под формата на таблица (серия на разпределение на вероятностите), аналитично и графично (многоъгълник на разпределение на вероятностите).

Когато се провежда експеримент, става необходимо да се оцени стойността, която се изследва „средно“. Ролята на средна стойност на случайна величина играе числова характеристика, наречена математическо очакване,което се определя по формулата

Където х 1 , х 2 ,.. , х н– стойности на случайни променливи х, А стр 1 ,стр 2 , ... , стр н– вероятностите на тези стойности (обърнете внимание, че стр 1 + стр 2 +…+ стр н = 1).

Пример. Стрелбата се извършва в целта (фиг. 11).

Попадение в I дава три точки, във II – две точки, в III – една точка. Броят точки, отбелязани в един изстрел от един стрелец, има закон за разпределение на формата

За да сравните уменията на стрелците, достатъчно е да сравните средните стойности на отбелязаните точки, т.е. математически очаквания М(х) И М(Y):

М(х) = 1 0,4 + 2  0,2 + 3  0,4 = 2,0,

М(Y) = 1 0,2 + 2  0,5 + 3  0,3 = 2,1.

Вторият стрелец дава средно малко по-голям брой точки, т.е. ще даде по-добри резултати при многократно задействане.

Нека отбележим свойствата на математическото очакване:

1. Математическото очакване на постоянна стойност е равно на самата константа:

М(° С) =C.

2. Математическото очакване на сумата от случайни променливи е равно на сумата от математическите очаквания на членовете:

М=(х 1 + х 2 +…+ х н)= М(х 1)+ М(х 2)+…+ М(х н).

3. Математическото очакване на произведението на взаимно независими случайни величини е равно на произведението на математическите очаквания на факторите

М(х 1 х 2 … х н) = М(х 1)М(х 2)… М(х н).

4. Математическото отрицание на биномното разпределение е равно на произведението от броя опити и вероятността събитие да се случи в едно изпитване (задача 4.6).

М(х) = пр.

За да се оцени как една случайна променлива „средно“ се отклонява от своето математическо очакване, т.е. За да се характеризира разпространението на стойностите на случайна променлива в теорията на вероятностите, се използва концепцията за дисперсия.

Дисперсияслучайна величина хсе нарича математическо очакване на квадрата на отклонението:

д(х) = М[(х - М(х)) 2 ].

Дисперсията е числена характеристика на дисперсията на случайна променлива. От дефиницията става ясно, че колкото по-малка е дисперсията на една случайна променлива, толкова по-близко нейните възможни стойности са разположени около математическото очакване, т.е. по-добри стойностислучайната променлива се характеризира със своето математическо очакване.

От дефиницията следва, че дисперсията може да се изчисли по формулата

.

Удобно е дисперсията да се изчисли по друга формула:

д(х) = М(х 2) - (М(х)) 2 .

Дисперсията има следните свойства:

1. Дисперсията на константата е нула:

д(° С) = 0.

2. Константният фактор може да бъде изваден от знака на дисперсията чрез повдигане на квадрат:

д(CX) = ° С 2 д(х).

3. Дисперсията на сумата от независими случайни променливи е равна на сумата от дисперсията на членовете:

д(х 1 + х 2 + х 3 +…+ х н)= д(х 1)+ д(х 2)+…+ д(х н)

4. Дисперсията на биномното разпределение е равна на произведението от броя на опитите и вероятността за настъпване и ненастъпване на събитие в един опит:

д(х) = npq.

В теорията на вероятностите често се използва числова характеристика, равна на корен квадратен от дисперсията на случайна променлива. Тази числена характеристика се нарича средно квадратично отклонение и се обозначава със символа

.

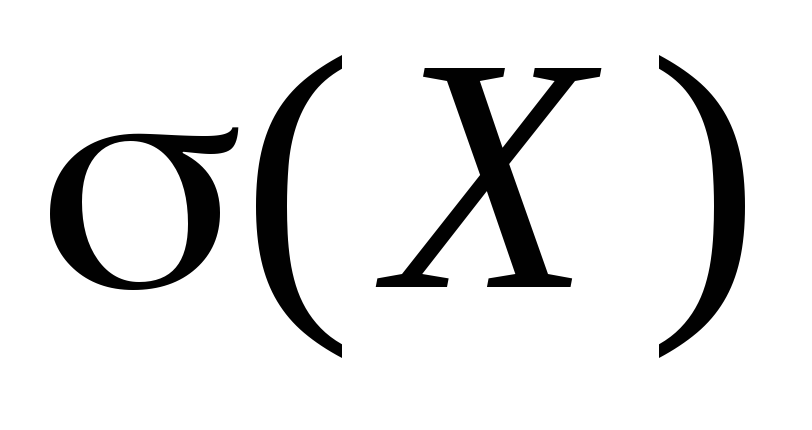Той характеризира приблизителния размер на отклонението на случайна величина от средната й стойност и има същата размерност като случайната величина.

4.1. Стрелецът стреля три пъти по целта. Вероятността за попадение в целта с всеки изстрел е 0,3.

Изградете серия за разпределение на броя на попаденията.

Решение. Броят на попаденията е дискретна случайна променлива х. Всяка стойност х н случайна величина хсъответства на определена вероятност П н .

Законът за разпределение на дискретна случайна променлива в този случай може да бъде специфициран близко разпространение.

В този проблем хприема стойности 0, 1, 2, 3. Според формулата на Бернули

,

Нека намерим вероятностите на възможните стойности на случайната променлива:

Р 3 (0) = (0,7) 3 = 0,343,

Р 3 (1) =0,3(0,7) 2 = 0,441,

Р 3 (2) =(0,3) 2 0,7 = 0,189,

Р 3 (3) = (0,3) 3 = 0,027.

Чрез подреждане на стойностите на случайната променлива хв нарастващ ред получаваме серията на разпределение:

х н

Имайте предвид, че сумата

означава вероятността случайната променлива хще приеме поне една стойност измежду възможните и следователно това събитие е надеждно

.

4.2 .В урната има четири топки с номера от 1 до 4. Изваждат се две топки. Случайна стойност х– сумата от числата на топките. Конструирайте серия на разпределение на случайна променлива х.

Решение.Стойности на случайни променливи хса 3, 4, 5, 6, 7. Нека намерим съответните вероятности. Стойност на случайна променлива 3 хможе да се приеме само в случай, когато една от избраните топки е с номер 1, а другата 2. Броят на възможните резултати от теста е равен на броя на комбинациите от четири (броя на възможните двойки топки) от две.

Използвайки класическата вероятностна формула, получаваме

по същия начин

Р(х= 4) =Р(х= 6) =Р(х= 7) = 1/6.

Сборът 5 може да се появи в два случая: 1 + 4 и 2 + 3, така че

.

хима формата:

Намерете функцията на разпределение Е(х) случайна величина хи го начертайте. Изчислете за хнеговото математическо очакване и дисперсия.

Решение. Законът за разпределение на случайна променлива може да бъде определен чрез функцията на разпределение

Е(х) =P(х х).

Разпределителна функция Е(х) е ненамаляваща, ляво-непрекъсната функция, дефинирана на цялата числова ос, докато

Е (- )= 0,Е (+ )= 1.

За дискретна случайна променлива тази функция се изразява с формулата

.

Следователно в този случай

Графика на функцията на разпределение Е(х) е стъпаловидна линия (фиг. 12)

	Е(х)

Очаквана стойностМ(х) е среднопретеглената аритметична стойност на стойностите х 1 , Х 2 ,……Х нслучайна величина хс везни ρ 1, ρ 2, …… , ρ н и се нарича средна стойност на случайната променлива х. Според формулата

М(х)= х 1 ρ 1 + x 2 ρ 2 +……+ x н ρ н

М(х) = 3·0,14+5·0,2+7·0,49+11·0,17 = 6,72.

дисперсияхарактеризира степента на дисперсия на стойностите на случайна променлива от нейната средна стойност и се обозначава д(х):

д(х)=М[(HM(х)) 2 ]= М(х 2) –[М(х)] 2 .

За дискретна случайна променлива дисперсията има формата

или може да се изчисли с помощта на формулата

Замествайки числените данни на проблема във формулата, получаваме:

М(х 2) = 3 2 ∙ 0,14+5 2 ∙ 0,2+7 2 ∙ 0,49+11 2 ∙ 0,17 = 50,84

д(х) = 50,84-6,72 2 = 5,6816.

4.4. Два зара се хвърлят два пъти едновременно. Напишете биномиалния закон за разпределение на дискретна случайна променлива х- броят на срещанията на четен общ брой точки на два зара.

Решение. Нека представим едно случайно събитие

А= (два зара с едно хвърляне доведоха до общ четен брой точки).

Използвайки класическата дефиниция на вероятността, намираме

Р(А)= ,

Където н - броят на възможните резултати от теста се намира според правилото

умножение:

н = 6∙6 =36,

м - брой хора, подкрепящи събитието Арезултати - равни

м= 3∙6=18.

По този начин вероятността за успех в едно изпитание е

ρ = П(А)= 1/2.

Задачата се решава с помощта на тестова схема на Бернули. Едно предизвикателство тук ще бъде хвърлянето на два зара веднъж. Брой такива тестове н = 2. Случайна променлива хприема стойности 0, 1, 2 с вероятности

Р 2 (0) =,Р 2 (1) =∙,Р 2 (2) =

Изискваното биномно разпределение на случайна променлива хможе да се представи като серия на разпространение:

х н
ρ н

4.5 . В партида от шест части има четири стандартни части. Три части бяха избрани на случаен принцип. Конструирайте вероятностно разпределение на дискретна случайна променлива х– броя на стандартните части сред избраните и намиране на математическото му очакване.

Решение.Стойности на случайни променливи хса числата 0,1,2,3. Това е ясно Р(х=0)=0, тъй като има само две нестандартни части.

Р(х=1) =
=1/5,

Р(X= 2) =
= 3/5,

Р(х=3) =
= 1/5.

Закон за разпределение на случайна величина хНека го представим под формата на серия за разпространение:

х н
ρ н

Очаквана стойност

М(х)=1 ∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2.

4.6 . Докажете, че математическото очакване на дискретна случайна променлива х- брой появявания на събитието А V ннезависими опити, при всяко от които вероятността за настъпване на събитие е равна на ρ – равно на произведението на броя опити по вероятността за настъпване на събитие в едно изпитване, т.е. да се докаже, че математическото очакване на биномното разпределение

М(х) =н . ρ ,

и дисперсия

д(х) =н.п. .

Решение.Случайна стойност хможе да приема стойности 0, 1, 2..., н. Вероятност Р(х= k) се намира по формулата на Бернули:

Р(х=к)= Р н(k)= ρ Да се (1-ρ ) н-Да се

Серия на разпределение на случайна променлива хима формата:

х н
ρ н	р н	ρq н- 1	ρq н- 2		ρ н

Където р= 1- ρ .

За математическото очакване имаме израза:

М(х)=ρq н - 1 +2 ρ 2 р н - 2 +…+.н ρ н

В случай на един тест, тоест с n= 1 за случайна променлива х 1 – брой повторения на събитието А- серията на разпределение има формата:

х н
ρ н

М(х 1)= 0∙q + 1 ∙ стр = стр

д(х 1) = стр – стр 2 = стр(1- стр) = pq.

Ако х k – брой повторения на събитието Ав кой тест тогава Р(х Да се)= ρ И

X=X 1 +X 2 +….+X н .

От тук получаваме

М(х)=М(х 1 )+М(х 2)+ … +М(х н)= nρ,

д(х)=D(х 1)+D(х 2)+ ... +D(х н)=npq.

4.7. Отделът за контрол на качеството проверява продуктите за стандартност. Вероятността продуктът да е стандартен е 0,9. Всяка партида съдържа 5 продукта. Намерете математическото очакване на дискретна случайна променлива х- броя на партидите, всяка от които ще съдържа 4 стандартни продукта - ако на проверка подлежат 50 партиди.

Решение. Вероятността във всяка произволно избрана партида да има 4 стандартни продукта е постоянна; нека го обозначим с ρ .Тогава математическото очакване на случайната променлива хравно на М(х)= 50∙ρ.

Нека намерим вероятността ρ според формулата на Бернули:

ρ=P 5 (4)== 0,94∙0,1=0,32.

М(х)= 50∙0,32=16.

4.8 . Хвърлят се три зара. Намерете математическото очакване на сбора от падналите точки.

Решение.Можете да намерите разпределението на случайна променлива х- сумата на падналите точки и след това нейното математическо очакване. Този път обаче е твърде тромав. По-лесно е да се използва друга техника, представляваща случайна променлива х, чието математическо очакване трябва да се изчисли, под формата на сума от няколко по-прости случайни променливи, чието математическо очакване е по-лесно за изчисляване. Ако случайната променлива х азе броят на падналите точки аз– та кости ( аз= 1, 2, 3), след това сумата от точките хще се изрази във формата

X = X 1 + X 2 + X 3 .

За да се изчисли математическото очакване на оригиналната случайна променлива, всичко, което остава, е да се използва свойството на математическото очакване

М(х 1 + X 2 + X 3 )= М(х 1 )+ М(х 2)+ М(х 3 ).

Това е очевидно

Р(х аз = К)= 1/6, ДА СЕ= 1, 2, 3, 4, 5, 6, аз= 1, 2, 3.

Следователно, математическото очакване на случайната променлива х азизглежда като

М(х аз) = 1/6∙1 + 1/6∙2 +1/6∙3 + 1/6∙4 + 1/6∙5 + 1/6∙6 = 7/2,

М(х) = 3∙7/2 = 10,5.

4.9. Определете математическото очакване на броя устройства, които са се провалили по време на тестването, ако:

а) вероятността от повреда за всички устройства е еднаква Р, а броят на тестваните устройства е равен на н;

б) вероятност за провал за аз – на устройството е равно на стр аз , аз= 1, 2, … , н.

Решение.Нека случайната променлива хтогава е броят на неуспешните устройства

X = X 1 + X 2 + … + X н ,

х аз =

Това е ясно

Р(х аз = 1)= Р аз , Р(х аз = 0)= 1– Р аз ,i= 1, 2, … ,н.

М(х аз)= 1∙Р аз + 0∙(1-Р аз)=P аз ,

М(х)=М(х 1)+М(х 2)+ … +М(х н)=P 1 +P 2 + … + П н .

В случай "а" вероятността от повреда на устройството е същата, т.е

Р аз =стр,i= 1, 2, … ,н.

М(х)= н.п..

Този отговор може да бъде получен веднага, ако забележим, че случайната променлива хТо има биномно разпределениес параметри ( н, стр).

4.10. Два зара се хвърлят едновременно два пъти. Напишете биномиалния закон за разпределение на дискретна случайна променлива Х -броят на хвърлянията на четен брой точки на два зара.

Решение. Позволявам

А=(хвърляне на четно число на първия зар),

B =(хвърляне на четно число на втория зар).

Получаването на четно число на двата зара с едно хвърляне се изразява чрез произведението AB.Тогава

Р (AB) = Р(А)∙Р(IN) =
.

Резултатът от второто хвърляне на два зара не зависи от първото, така че формулата на Бернули се прилага, когато

н = 2,p = 1/4, р = 1– p = 3/4.

Случайна стойност хможе да приема стойности 0, 1, 2 , вероятността за което може да се намери с помощта на формулата на Бернули:

Р(X= 0)= П 2 (0) = р 2 = 9/16,

Р(X= 1)= П 2 (1)= В ,Р∙р = 6/16,

Р(X= 2)= П 2 (2)= В , Р 2 = 1/16.

Серия на разпределение на случайна променлива Х:

4.11. Устройството се състои от голям брой независимо работещи елементи с една и съща много малка вероятност от повреда на всеки елемент във времето T. Намерете средния брой откази за времето Tелементи, ако вероятността поне един елемент да се повреди през това време е 0,98.

Решение. Брой хора, отказали във времето Tелементи – случайна величина х, който се разпределя по закона на Поасон, тъй като броят на елементите е голям, елементите работят независимо и вероятността от повреда на всеки елемент е малка. Средният брой повторения на събитие в нтестове е равно

М(х) = н.п..

Тъй като вероятността от провал ДА СЕелементи от низразено с формулата

Р н (ДА СЕ)
,

където  = н.п., тогава вероятността нито един елемент да не се повреди през това време T получаваме К = 0:

Р н (0)= д -  .

Следователно вероятността за обратното събитие е във времето T поне един елемент е неуспешен – равен на 1 - д -  . Според условията на задачата тази вероятност е 0,98. От ур.

1 - д -  = 0,98,

д -  = 1 – 0,98 = 0,02,

от тук  = -вътре 0,02  4.

И така, във времето Tработа на устройството, средно 4 елемента ще се повредят.

4.12 . Заровете се хвърлят, докато се появи „две“. Намерете средния брой хвърляния.

Решение. Нека въведем случайна променлива х– броя тестове, които трябва да бъдат извършени до настъпване на интересуващото ни събитие. Вероятността, че х= 1 е равна на вероятността при едно хвърляне на зара да се появи „двойка“, т.е.

Р(X= 1) = 1/6.

Събитие х= 2 означава, че при първия тест „двойката“ не е излязла, но при втория се е получила. Вероятност за събитие х= 2 се намира по правилото за умножаване на вероятностите за независими събития:

Р(X= 2) = (5/6)∙(1/6)

по същия начин

Р(X= 3) = (5/6) 2 ∙1/6, Р(X= 4) = (5/6) 2 ∙1/6

и т.н. Получаваме серия от вероятностни разпределения:

					(5/6) Да се ∙1/6

Средният брой хвърляния (изпитания) е математическото очакване

М(х) = 1∙1/6 + 2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6 + … + ДА СЕ (5/6) ДА СЕ -1 ∙1/6 + … =

1/6∙(1+2∙5/6 +3∙(5/6) 2 + … + ДА СЕ (5/6) ДА СЕ -1 + …)

Нека намерим сумата на серията:

ДА СЕж ДА СЕ -1 = (ж ДА СЕ) ж 
.

следователно

М(х) = (1/6) (1/ (1 – 5/6) 2 = 6.

По този начин трябва да направите средно 6 хвърляния на зара, докато се появи „две“.

4.13. Провеждат се независими тестове със същата вероятност за възникване на събитието Авъв всеки тест. Намерете вероятността за възникване на събитие А, ако дисперсията на броя на появяванията на събитие в три независими опита е 0,63 .

Решение.Броят на случванията на събитие в три опита е случайна променлива х, разпределени по биномния закон. Дисперсията на броя на случаите на събитие в независими опити (с една и съща вероятност за възникване на събитието във всеки опит) е равна на произведението на броя на опитите с вероятностите за възникване и ненастъпване на събитието (задача 4.6)

д(х) = npq.

По условие н = 3, д(х) = 0,63, така че можете Рнамерете от уравнението

0,63 = 3∙Р(1-Р),

който има две решения Р 1 = 0,7 и Р 2 = 0,3.

Дадена е серия на разпределение на дискретна случайна променлива. Намерете липсващата вероятност и начертайте функцията на разпределение. Изчислете математическото очакване и дисперсията на това количество.

Случайната променлива X приема само четири стойности: -4, -3, 1 и 2. Тя приема всяка от тези стойности с определена вероятност. Тъй като сумата от всички вероятности трябва да е равна на 1, липсващата вероятност е равна на:

0,3 + ? + 0,1 + 0,4 = 1,

Нека съставим функцията на разпределение на случайната променлива X. Известно е, че функцията на разпределение , тогава:

следователно

Нека начертаем функцията Е(х) .

Математическото очакване на дискретна случайна променлива е равно на сумата от произведенията на стойността на случайната променлива и съответната вероятност, т.е.

Намираме дисперсията на дискретна случайна променлива по формулата:

ПРИЛОЖЕНИЕ

Елементи на комбинаториката Тук: - факториел на число

Действия върху събития Събитие е всеки факт, който може или не може да се случи в резултат на преживяване. Обединяване на събития АИ IN- това събитие СЪСкоето се състои от външен вид или събитие А, или събития IN, или и двете събития едновременно. Обозначаване: ; Пресичащи събития АИ IN- това събитие СЪС, което се състои от едновременното настъпване на двете събития. Обозначаване: ;

Класическа дефиниция на вероятността Вероятност за събитие Ае отношението на броя на експериментите , благоприятни за настъпване на събитие А, Да се общ бройексперименти :

Формула за умножение на вероятностите Вероятност за събитие може да се намери с помощта на формулата: - вероятност за събитие а, - вероятност за събитие IN, - вероятност за събитие INпри условие, че събитието Авече се е случило. Ако събития A и B са независими (настъпването на едното не влияе върху настъпването на другото), тогава вероятността за събитието е равна на:

Формула за добавяне на вероятности Вероятност за събитие може да се намери с помощта на формулата: Вероятност за събитие а, Вероятност за събитие IN, - вероятност за едновременно протичане на събития АИ IN. Ако събития A и B са несъвместими (не могат да се случат едновременно), тогава вероятността за събитието е равна на:

Формула за пълна вероятност Нека събитието Аможе да се случи едновременно с едно от събитията , , …, - нека ги наречем хипотези. Също известен - вероятност за изпълнение аз-та хипотеза и - вероятност за възникване на събитие А при изпълнение аз-та хипотеза. Тогава вероятността от събитието Аможе да се намери по формулата:

Схема на Бернули Нека n независими тестове. Вероятност за настъпване (успех) на събитие Авъв всяка от тях е постоянна и равна стр, вероятността от повреда (т.е. събитието да не се случи А) р = 1 - стр. След това вероятността за поява куспех в нтестовете могат да бъдат намерени с помощта на формулата на Бернули: Най-вероятният брой успехи в схемата на Бернули това е броят на случванията на определено събитие, което има най-висока вероятност. Може да се намери с помощта на формулата:

Случайни променливи дискретно непрекъснато (например броят на момичетата в семейство с 5 деца) (например времето, в което чайникът работи правилно) Числени характеристики на дискретни случайни величини Нека дискретно количество е дадено от серия на разпределение: х Р , , …, - стойности на случайна променлива х; , , …, са съответните вероятностни стойности. Разпределителна функция Функция на разпределение на случайна величина хе функция, дефинирана на цялата числова ос и равна на вероятността, че хще има по-малко х:

Въпроси за изпита

Събитие.

Операции върху случайни събития.

Концепцията за вероятността от събитие.

Правила за събиране и умножение на вероятности. Условни вероятности.

Формула за пълна вероятност. Формула на Бейс.

Схема на Бернули.

Случайна променлива, нейната функция на разпределение и ред на разпределение.

Основни свойства на функцията на разпределение.

Очаквана стойност. Свойства на математическото очакване.

дисперсия.

Свойства на дисперсията.

Плътност на разпределение на вероятността на едномерна случайна променлива. Видове разпределения: равномерно, експоненциално, нормално, биномно и Поасоново разпределение.Местни и

интегрални теореми

Моавр-Лаплас.

Закон и функция на разпределение на система от две случайни величини.

Зависими и независими случайни променливи. Коефициент на корелация.

проба.

Обработка на проби. Многоъгълна и честотна хистограма. Емпирична функция на разпределение.

Концепцията за оценка на параметрите на разпределението. Изисквания към оценката. Доверителен интервал. Конструиране на интервали за оценка на математическото очакване и стандартното отклонение.

Статистически хипотези. Критерии за съгласие.Случайна величина е променлива, която в резултат на всеки опит взема едно нещо предварителнонеизвестна стойност , в зависимост от случайни причини. Случайните променливи се означават с главни латински букви: $X,\ Y,\ Z,\ \dots $ Според вида си случайните променливи могат да бъдатИ отделен.

непрекъснатоДискретна случайна променлива

- това е случайна променлива, чиито стойности не могат да бъдат повече от изброими, т.е. крайни или изброими. Под изброимост имаме предвид, че стойностите на случайна променлива могат да бъдат номерирани. Пример 1

. Ето примери за дискретни случайни променливи:

а) броят на попаденията в целта с $n$ изстрела, тук възможните стойности са $0,\ 1,\ \dots ,\ n$.

б) броят на падналите емблеми при хвърляне на монета, тук възможните стойности са $0,\ 1,\ \dots ,\ n$.

в) броя на корабите, пристигащи на борда (изброим набор от стойности).

г) броят на повикванията, пристигащи в телефонната централа (изброим набор от стойности).

1. Закон за вероятностно разпределение на дискретна случайна променлива. Дискретна случайна променлива $X$ може да приема стойности $x_1,\dots ,\ x_n$ с вероятности $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. Съответствието между тези стойности и техните вероятности се наричазакон за разпределение на дискретна случайна променлива

. По правило това съответствие се посочва с помощта на таблица, чийто първи ред показва стойностите $x_1,\dots ,\ x_n$, а вторият ред съдържа вероятностите $p_1,\dots ,\ p_n$, съответстващи на тези ценности.
$\begin(масив)(|c|c|)
\hline
$\begin(масив)(|c|c|)
X_i & x_1 & x_2 & \dots & x_n \\
$\begin(масив)(|c|c|)
p_i & p_1 & p_2 & \dots & p_n \\

\край (масив)$ Пример 2 . Нека случайната променлива $X$ е броят точки, паднали по време на хвърлянетозарове

. По правило това съответствие се посочва с помощта на таблица, чийто първи ред показва стойностите $x_1,\dots ,\ x_n$, а вторият ред съдържа вероятностите $p_1,\dots ,\ p_n$, съответстващи на тези ценности.
$\begin(масив)(|c|c|)
1 & 2 & 3 & 4 & 5 & 6 \\
$\begin(масив)(|c|c|)

$\begin(масив)(|c|c|)
p_i & p_1 & p_2 & \dots & p_n \\

. Такава случайна променлива $X$ може да приема следните стойности: $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Вероятностите за всички тези стойности са равни на $1/6$. Тогава законът за разпределение на вероятностите на случайната променлива $X$:Коментирайте

2. Математическо очакване на дискретна случайна променлива.

Очакване на случайна променливазадава своето „централно“ значение. За дискретна случайна променлива, математическото очакване се изчислява като сумата от продуктите на стойностите $x_1,\dots ,\ x_n$ и вероятностите $p_1,\dots ,\ p_n$, съответстващи на тези стойности, т.е. : $M\left(X\right)=\sum ^n_(i=1)(p_ix_i)$. В англоезичната литература се използва друга нотация $E\left(X\right)$.

Свойства на математическото очакване$M\ляво(X\дясно)$:

1. $M\left(X\right)$ се съдържа между най-малкото и най-високи стойностислучайна променлива $X$.
2. Математическото очакване на константа е равно на самата константа, т.е. $M\ляво(C\дясно)=C$.
3. Постоянният фактор може да бъде изваден от знака на математическото очакване: $M\left(CX\right)=CM\left(X\right)$.
4. Математическото очакване на сумата от случайни променливи е равно на сумата от техните математически очаквания: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
5. Математическото очакване на произведението на независими случайни променливи е равно на произведението на техните математически очаквания: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.

Пример 3 . Нека намерим математическото очакване на случайната променлива $X$ от пример $2$.

$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\над (6))+4\cdot ((1)\над (6))+5\cdot ((1)\над (6))+6\cdot ((1 )\над (6))=3,5.$$

Можем да забележим, че $M\left(X\right)$ се намира между най-малката ($1$) и най-голямата ($6$) стойности на случайната променлива $X$.

Пример 4 . Известно е, че математическото очакване на случайната променлива $X$ е равно на $M\left(X\right)=2$. Намерете математическото очакване на случайната променлива $3X+5$.

Използвайки горните свойства, получаваме $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\ cdot 2 +5=$11.

Пример 5 . Известно е, че математическото очакване на случайната променлива $X$ е равно на $M\left(X\right)=4$. Намерете математическото очакване на случайната променлива $2X-9$.

Използвайки горните свойства, получаваме $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\ cdot 4 -9=-1$.

3. Дисперсия на дискретна случайна променлива.

Възможните стойности на случайни променливи с еднакви математически очаквания могат да се разпръснат по различен начин около техните средни стойности. Например в две ученически групи общ успехза изпита по теория на вероятностите се оказа равна на 4, но в едната група всички се оказаха добри, а в другата - само тройки и отличници. Следователно има нужда от числена характеристика на случайна променлива, която да показва разпространението на стойностите на случайната променлива около нейното математическо очакване. Тази характеристика е дисперсия.

Дисперсия на дискретна случайна променлива$X$ е равно на:

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2).\ $$

В англоезичната литература се използва обозначението $V\left(X\right),\ Var\left(X\right)$. Много често дисперсията $D\left(X\right)$ се изчислява по формулата $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\ ляво(X \дясно)\дясно))^2$.

Дисперсионни свойства$D\ляво(X\дясно)$:

1. Дисперсията винаги е по-голяма или равна на нула, т.е. $D\наляво(X\надясно)\ge 0$.
2. Дисперсията на константата е нула, т.е. $D\ляво(C\дясно)=0$.
3. Константният фактор може да бъде изваден от знака на дисперсията, при условие че е повдигнат на квадрат, т.е. $D\left(CX\right)=C^2D\left(X\right)$.
4. Дисперсията на сумата от независими случайни променливи е равна на сумата от техните дисперсии, т.е. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
5. Дисперсията на разликата между независими случайни променливи е равна на сумата от техните дисперсии, т.е. $D\ляво(X-Y\дясно)=D\ляво(X\дясно)+D\ляво(Y\дясно)$.

Пример 6 . Нека изчислим дисперсията на случайната променлива $X$ от пример $2$.

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\над (6))\cdot (\left(1-3.5\right))^2+(((1)\over (6))\cdot (\left(2-3.5\right))^2+ \dots +( (1)\над (6))\cdot (\left(6-3.5\right))^2=((35)\над (12))\приблизително 2,92.$$

Пример 7 . Известно е, че дисперсията на случайната променлива $X$ е равна на $D\left(X\right)=2$. Намерете дисперсията на случайната променлива $4X+1$.

Използвайки горните свойства, намираме $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0= 16D\ ляво(X\дясно)=16\cdot 2=32$.

Пример 8 . Известно е, че дисперсията на случайната променлива $X$ е равна на $D\left(X\right)=3$. Намерете дисперсията на случайната променлива $3-2X$.

Използвайки горните свойства, намираме $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)= 4D\ ляво(X\дясно)=4\cdot 3=12$.

4. Функция на разпределение на дискретна случайна величина.

Методът за представяне на дискретна случайна променлива под формата на серия на разпределение не е единственият и най-важното е, че не е универсален, тъй като непрекъсната случайна променлива не може да бъде определена с помощта на серия на разпределение. Има и друг начин за представяне на случайна променлива - функцията на разпределение.

Разпределителна функцияслучайна променлива $X$ се нарича функция $F\left(x\right)$, която определя вероятността случайната променлива $X$ да приеме стойност, по-малка от някаква фиксирана стойност $x$, т.е. $F\ ляво(x\дясно)=P\ляво(X< x\right)$

Свойства на функцията на разпределение:

1. $0\le F\left(x\right)\le 1$.
2. Вероятността случайната променлива $X$ да приеме стойности от интервала $\left(\alpha ;\ \beta \right)$ е равна на разликата между стойностите на функцията на разпределение в краищата на този интервал: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
3. $F\left(x\right)$ - ненамаляващ.
4. $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$.

Пример 9 . Нека намерим функцията на разпределение $F\left(x\right)$ за закона за разпределение на дискретната случайна променлива $X$ от пример $2$.

. По правило това съответствие се посочва с помощта на таблица, чийто първи ред показва стойностите $x_1,\dots ,\ x_n$, а вторият ред съдържа вероятностите $p_1,\dots ,\ p_n$, съответстващи на тези ценности.
$\begin(масив)(|c|c|)
1 & 2 & 3 & 4 & 5 & 6 \\
$\begin(масив)(|c|c|)
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
$\begin(масив)(|c|c|)
p_i & p_1 & p_2 & \dots & p_n \\

Ако $x\le 1$, тогава очевидно $F\left(x\right)=0$ (включително за $x=1$ $F\left(1\right)=P\left(X< 1\right)=0$).

Ако $1< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.

Ако $2< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.

Ако $3< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.

Ако $4< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.

Ако $5< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.

Ако $x > 6$, тогава $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right) +P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+ 1/6+1/6=1$.

Така че $F(x)=\left\(\begin(matrix)
0,\ при\ x\le 1,\\
1/6, при \ 1< x\le 2,\\
1/3,\ на\ 2< x\le 3,\\
1/2, при \ 3< x\le 4,\\
2/3,\ в\ 4< x\le 5,\\
5/6,\ в\ 4< x\le 5,\\
1,\ за\ x > 6.
\end(матрица)\right.$