Дисперсия (разсейване) на случайна променлива е математическото очакване на квадрата на отклонението на случайна променлива от нейното математическо очакване:
За да изчислите дисперсията, можете да използвате леко модифицирана формула
защото M(X), 2 и 
– постоянни стойности. По този начин,
4.2.2. Дисперсионни свойства
Имот 1.Дисперсията на постоянна стойност е нула. Наистина, по дефиниция
Имот 2.Константният фактор може да бъде изваден от знака на дисперсията чрез повдигането му на квадрат.
Доказателство
Центрирано случайна променлива е отклонението на случайна променлива от нейното математическо очакване:
Центрираното количество има две свойства, удобни за трансформация:
Имот 3.Ако случайните променливи X и Yзначи са независими
Доказателство. Нека обозначим 
. Тогава.
Във втория член, поради независимостта на случайните променливи и свойствата на центрираните случайни променливи
Пример 4.5.Ако аИ b– константи, тогаваD (аX+b)=
д(аX)+д(b)=
.
4.2.3. Стандартно отклонение
Дисперсията, като характеристика на разпространението на случайна променлива, има един недостатък. ако напр. х– грешката на измерване има размерност ММ, тогава дисперсията има размерността 
. Поради това те често предпочитат да използват друга характеристика на разсейване - стандартно отклонение
, което е равно на корен квадратен от дисперсията
Стандартното отклонение има същото измерение като себе си произволна стойност.
Пример 4.6.Вариация на броя на появяванията на събитие в независим дизайн на изпитване
Произведено ннезависими опити и вероятността за възникване на събитие във всеки опит е Р. Нека изразим, както преди, броя на случванията на събитието хчрез броя на появяванията на събитието в отделните експерименти:
Тъй като експериментите са независими, случайните променливи, свързани с експериментите 
независима. И поради независимостта 
ние имаме
Но всяка от случайните променливи има закон на разпределение (пример 3.2)
|
| ||
И 
(пример 4.4). Следователно, по дефиниция на дисперсия:
Където р=1- стр.
В резултат на това имаме 
,
Стандартно отклонение на броя на случванията на събитие в ннезависими експерименти равни 
.
4.3. Моменти на случайни променливи
В допълнение към вече разгледаните, случайните променливи имат много други числени характеристики.
Началният момент
к х
(
) се нарича математическо очакване к-та степен на тази случайна променлива.
Централен момент кслучайна променлива от ти ред хнаречено математическо очакване к-та степен на съответната центрирана величина.
Лесно се вижда, че централният момент от първи ред винаги е равен на нула, централният момент от втори ред е равен на дисперсията, тъй като .
Централният момент от трети ред дава представа за асиметрията на разпределението на случайна променлива. Моментите на ред, по-висок от втория, се използват сравнително рядко, така че ще се ограничим само до самите понятия.
4.4. Примери за намиране на закони за разпределение
Нека разгледаме примери за намиране на законите за разпределение на случайни променливи и техните числени характеристики.
Пример 4.7.
Съставете закон за разпределение на броя на попаденията в мишена с три изстрела в мишена, ако вероятността за попадение с всеки изстрел е 0,4. Намерете интегралната функция Е(Х)за полученото разпределение на дискретна случайна променлива хи начертайте графика за него. Намерете очакваната стойност М(х)
, дисперсия д(х)
и стандартно отклонение 
(х) случайна величина х.
Решение
1) Дискретна случайна променлива х– броят на попаденията в целта с три изстрела – може да приема четири стойности: 0, 1, 2, 3 . Вероятността тя да приеме всеки от тях се намира с помощта на формулата на Бернули с: н=3,стр=0,4,р=1- стр=0,6 и м=0, 1, 2, 3:
Нека получим вероятностите на възможните стойности х:;
Нека съставим желания закон за разпределение на случайна променлива х:
Контрола: 0,216+0,432+0,288+0,064=1.
Нека построим полигон на разпределение на получената случайна променлива х. За да направите това, в правоъгълната координатна система маркираме точките (0; 0.216), (1; 0.432), (2; 0.288), (3; 0.064). Нека свържем тези точки с прави сегменти, получената начупена линия е желаният разпределителен многоъгълник (фиг. 4.1).
2) Ако x 
0, тогава Е(Х)=0. Наистина, за стойности, по-малки от нула, стойността хне приема. Следователно за всички х
0, използвайки дефиницията Е(Х), получаваме Е(Х)=П(х<
х)
=0 (като вероятност за невъзможно събитие).
Ако 0 
, Че Е(х)
=0,216. Наистина, в този случай Е(Х)=П(х<
х)
=
=П(-
<
х 
0)+
П(0<
х<
х)
=0,216+0=0,216.
Ако вземем напр. х=0,2, тогава Е(0,2)=П(х<0,2) . Но вероятността от събитие х<0,2 равна 0,216, так как случайная величинахсамо в един случай приема стойност по-малка от 0,2, а именно 0 с вероятност 0,216.
Ако 1 
, Че
Наистина ли, хможе да приеме стойност 0 с вероятност 0,216 и стойност 1 с вероятност 0,432; следователно едно от тези значения, без значение кое, хможе да приеме (според теоремата за събиране на вероятности от несъвместими събития) с вероятност от 0,648.
Ако 2 
, тогава, аргументирайки се по подобен начин, получаваме Е(Х)=0,216+0,432 + + 0,288=0,936. Наистина, нека напр. х=3. Тогава Е(3)=П(х<3)
изразява вероятността от събитие х<3 –
стрелок сделает меньше трех попаданий,
т.е. ноль, один или два. Применяя теорему
сложения вероятностей, получим указанное
значение функцииЕ(Х).
Ако х>3 тогава Е(Х)=0,216+0,432+0,288+0,064=1. Действително събитието х
е надежден и неговата вероятност е равна на единица, и х>3 – невъзможно. Като се има предвид това
Е(Х)=П(х<
х)
=П(х 
3)
+
П(3<
х<
х)
, получаваме посочения резултат.
Така се получава необходимата интегрална функция на разпределение на случайната променлива X:
Е(х)
=
чиято графика е показана на фиг. 4.2.
3) Математическото очакване на дискретна случайна променлива е равно на сумата от продуктите на всички възможни стойности хна техните вероятности:
M(X)=0=1,2.
Тоест средно има едно попадение в целта с три изстрела.
Дисперсията може да се изчисли от определението за дисперсия д(х)=
М(х-
М(х))
или използвайте формулата д(х)=
М(х 
, което води до целта по-бързо.
Нека напишем закона за разпределение на случайна променлива х 
:
Нека намерим математическото очакване за х
:
M(X 
)
= 04
= 2,16.
Нека изчислим необходимата дисперсия:
д(х)
=
М(х 
)
– (М(х))
= 2,16 – (1,2)
= 0,72.
Намираме стандартното отклонение с помощта на формулата
(х)
=
= 0,848.
Интервал ( М-
;
М+
) = (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – интервал от най-вероятните стойности на случайната променлива х, съдържа стойностите 1 и 2.
Пример 4.8.
Дадена е диференциална функция на разпределение (функция на плътност) на непрекъсната случайна променлива х:
f(х)
=
1) Определете постоянния параметър а.
2) Намерете интегралната функция Е(х) .
3) Изграждане на функционални графики f(х) И Е(х) .
4) Намерете вероятността по два начина P(0,5<
х 
1,5)
И П(1,5<
х<3,5)
.
5). Намерете очакваната стойност M(X), дисперсия д(Х)и стандартно отклонение 
случайна величина х.
Решение
1) Диференциална функция по свойство f(х)
трябва да отговаря на условието 
.
Нека изчислим този неправилен интеграл за тази функция f(х) :
Като заместим този резултат в лявата страна на равенството, получаваме това А=1. В условието за f(х)
заменете параметъра Аот 1: 
2) Да намериш Е(х) нека използваме формулата
.
Ако x 
, Че 
, следователно, 
Ако 1 
Че
Ако x>2, тогава
И така, търсената интегрална функция Е(х) има формата:
3) Да построим графики на функции f(х) И Е(х) (фиг. 4.3 и 4.4).
4) Вероятност случайна променлива да попадне в даден интервал (А,b)
изчислено по формулата 
, ако функцията е известна f(х),
и според формулата П(а
<
х
<
b)
=
Е(b)
–
Е(а),
ако функцията е известна
Е(х).
Ще намерим 
като използвате две формули и сравнете резултатите. По условие а=0,5;b=1,5;
функция f(х)
посочени в точка 1). Следователно търсената вероятност според формулата е равна на:
Същата вероятност може да се изчисли с помощта на формула b) чрез увеличението, получено в стъпка 2). интегрална функция Е(х) на този интервал:
защото Е(0,5)=0.
По същия начин намираме 
защото Е(3,5)=1.
5) Да се намери математическото очакване M(X)нека използваме формулата 
функция f(х)
дадено в решението на точка 1), е равно на нула извън интервала (1,2]:
Дисперсия на непрекъсната случайна променлива д(Х)се определя от равенството
, или еквивалентното равенство
.
За 
находка д(х)
Нека използваме последната формула и вземем предвид, че всички възможни стойности f(х)
принадлежат на интервала (1,2]:
Стандартно отклонение 
=
=0,276.
Интервал на най-вероятните стойности на случайна променлива хравно на
(М- 
,M+ 
)
= (1,58-0,28; 1,58+0,28) = (1,3; 1,86).
Дисперсия в статистикатасе намира като индивидуалните стойности на характеристиката на квадрат от . В зависимост от първоначалните данни се определя с помощта на формулите за проста и претеглена дисперсия:
1. (за негрупирани данни) се изчислява по формулата:
2. Претеглена дисперсия (за вариационни серии):
където n е честота (повторяемост на фактор X)
Пример за намиране на дисперсия
Тази страница описва стандартен пример за намиране на отклонение, можете също да разгледате други проблеми за намирането му
Пример 1. Следните данни са достъпни за група от 20 задочни студенти. Необходимо е да се изгради интервална серия от разпределението на характеристиката, да се изчисли средната стойност на характеристиката и да се изследва нейната дисперсия
Нека изградим интервално групиране. Нека определим обхвата на интервала, използвайки формулата:
където X max е максималната стойност на груповата характеристика;
X min – минимална стойност на груповия признак;
n – брой интервали:
Приемаме n=5. Стъпката е: h = (192 - 159)/ 5 = 6,6
Нека създадем интервално групиране
За по-нататъшни изчисления ще изградим спомагателна таблица:
X'i е средата на интервала. (например средата на интервала 159 – 165.6 = 162.3)
Определяме средния ръст на учениците, като използваме формулата за средноаритметично претеглено:
Нека определим дисперсията с помощта на формулата:
Формулата на дисперсията може да се трансформира, както следва:
От тази формула следва, че дисперсията е равна на разликата между средната стойност на квадратите на опциите и квадрата и средната стойност.
Дисперсия във вариационни сериис равни интервали, използвайки метода на моментите, може да се изчисли по следния начин, като се използва второто свойство на дисперсията (разделяне на всички опции на стойността на интервала). Определяне на дисперсия, изчислено по метода на моментите, като се използва следната формула е по-малко трудоемко:
където i е стойността на интервала;
А е конвенционална нула, за която е удобно да се използва средата на интервала с най-висока честота;
m1 е квадратът на момента от първи ред;
m2 - момент от втори ред
(ако в статистическа популация дадена характеристика се промени по такъв начин, че има само две взаимно изключващи се опции, тогава такава променливост се нарича алтернативна) може да се изчисли по формулата:
Замествайки q = 1- p в тази дисперсионна формула, получаваме:
Видове дисперсии
Обща дисперсияизмерва вариацията на дадена характеристика в цялата съвкупност като цяло под влиянието на всички фактори, които причиняват тази вариация. Тя е равна на средния квадрат на отклоненията на отделните стойности на характеристика x от общата средна стойност на x и може да се определи като проста дисперсия или претеглена дисперсия.
характеризира случайна вариация, т.е. част от вариацията, която се дължи на влиянието на неотчетени фактори и не зависи от фактора-атрибут, който формира основата на групата. Такава дисперсия е равна на средния квадрат на отклоненията на индивидуалните стойности на атрибута в групата X от средното аритметично на групата и може да се изчисли като проста дисперсия или като претеглена дисперсия.
По този начин, мерки за дисперсия в рамките на групатавариация на признак в група и се определя по формулата:
където xi е средното за групата;
ni е броят на единиците в групата.
Например вътрешногруповите отклонения, които трябва да бъдат определени в задачата за изследване на влиянието на квалификацията на работниците върху нивото на производителността на труда в цеха, показват отклонения в производството във всяка група, причинени от всички възможни фактори (техническо състояние на оборудването, наличие на инструменти и материали, възраст на работниците, интензивност на труда и др.), с изключение на разликите в квалификационната категория (в рамките на групата всички работници имат еднаква квалификация).
Средната стойност на дисперсиите в рамките на групата отразява случайно, т.е. онази част от вариацията, която е настъпила под влиянието на всички други фактори, с изключение на фактора за групиране. Изчислява се по формулата:
Характеризира систематичното изменение на получената характеристика, което се дължи на влиянието на фактора-атрибут, който формира основата на групата. Тя е равна на средния квадрат на отклоненията на груповите средни стойности от общата средна стойност. Междугруповата дисперсия се изчислява по формулата:
Правилото за добавяне на дисперсия в статистиката
Според правило за добавяне на отклоненияобщата дисперсия е равна на сумата от средната стойност на вътрешногруповите и междугруповите дисперсии:
Значението на това правилое, че общата дисперсия, която възниква под влиянието на всички фактори, е равна на сумата от дисперсиите, които възникват под влиянието на всички други фактори, и дисперсията, която възниква поради групиращия фактор.
Използвайки формулата за добавяне на дисперсии, можете да определите третата неизвестна дисперсия от две известни дисперсии и също така да прецените силата на влиянието на груповата характеристика.
Дисперсионни свойства
1. Ако всички стойности на дадена характеристика се намалят (увеличат) със същата постоянна сума, тогава дисперсията няма да се промени.
2. Ако всички стойности на дадена характеристика се намалят (увеличат) с еднакъв брой пъти n, тогава дисперсията съответно ще намалее (увеличи) с n^2 пъти.
Наред с изучаването на вариациите на дадена характеристика в цялата популация като цяло, често е необходимо да се проследят количествените промени в характеристиката в групите, на които е разделена популацията, както и между групите. Това изследване на вариация се постига чрез изчисляване и анализиране на различни видове вариация.
Има общи, междугрупови и вътрешногрупови дисперсии.
Обща дисперсия σ 2измерва вариацията на даден признак в цялата популация под влиянието на всички фактори, които са причинили тази вариация.
Междугруповата вариация (δ) характеризира систематичната вариация, т.е. разлики в стойността на изучавания признак, които възникват под влиянието на факторния признак, който формира основата на групата. Изчислява се по формулата: 
.
Дисперсия в рамките на групата (σ)отразява случайна вариация, т.е. част от вариацията, която възниква под влияние на неотчетени фактори и не зависи от фактора-атрибут, който формира основата на групата. Изчислява се по формулата: 
.
Средна стойност на дисперсиите в рамките на групата: 
.
Има закон, свързващ 3 вида дисперсия. Общата дисперсия е равна на сумата от средната стойност на вътрешногруповата и междугруповата дисперсия: 
.
Това съотношение се нарича правило за добавяне на отклонения.
Широко използван показател в анализа е делът на дисперсията между групите в общата дисперсия. Нарича се емпиричен коефициент на детерминация (η 2): .
Корен квадратен от емпиричния коефициент на детерминация се нарича емпирично съотношение на корелация (η):
.
Той характеризира влиянието на характеристиката, която формира основата на групата, върху вариацията на получената характеристика. Емпиричното съотношение на корелация варира от 0 до 1.
Нека демонстрираме практическата му употреба, като използваме следния пример (Таблица 1).
Пример №1. Таблица 1 - Производителност на труда на две групи работници в един от цеховете на НПО "Циклон"
Нека изчислим общите и груповите средни и дисперсии:
Изходните данни за изчисляване на средната стойност на вътрешногруповата и междугруповата вариация са представени в табл. 2.
таблица 2
Изчисление и δ 2 за две групи работници.
|
Работнически групи | Брой работници, хора | Средно, деца/смяна | дисперсия |
| Завършено техническо обучение | 5 | 95 | 42,0 |
| Тези, които не са завършили техническо обучение | 5 | 81 | 231,2 |
| Всички работници | 10 | 88 | 185,6 |
.
Междугрупова дисперсия
Общо отклонение:
По този начин емпиричното съотношение на корелация: .
Наред с вариациите в количествените характеристики могат да се наблюдават и вариации в качествените характеристики. Това изследване на вариацията се постига чрез изчисляване на следните видове вариации:
Вътрешногруповата дисперсия на дела се определя по формулата
Където n i– брой единици в отделни групи.Делът на изследваната характеристика в цялата популация, който се определя по формулата:
Трите вида дисперсии са свързани помежду си, както следва:
.
Тази връзка на дисперсиите се нарича теорема за добавяне на дисперсии на дела на признака.
Математическото очакване (средна стойност) на случайна променлива X, дадена в дискретно вероятностно пространство, е числото m =M[X]=∑x i p i, ако серията се сближава абсолютно.
Цел на услугата. Използване на онлайн услугата изчисляват се математическото очакване, дисперсията и стандартното отклонение(вижте примера). Освен това се начертава графика на функцията на разпределение F(X).
Свойства на математическото очакване на случайна величина
- Математическото очакване на константна стойност е равно на себе си: M[C]=C, C – константа;
- M=C M[X]
- Математическото очакване на сумата от случайните променливи е равно на сумата от техните математически очаквания: M=M[X]+M[Y]
- Математическото очакване на произведението на независими случайни променливи е равно на произведението на техните математически очаквания: M=M[X] M[Y] , ако X и Y са независими.
Дисперсионни свойства
- Дисперсията на постоянна стойност е нула: D(c)=0.
- Константният фактор може да бъде изваден от под знака на дисперсията, като го повдигнете на квадрат: D(k*X)= k 2 D(X).
- Ако случайните променливи X и Y са независими, тогава дисперсията на сумата е равна на сумата от дисперсиите: D(X+Y)=D(X)+D(Y).
- Ако случайните променливи X и Y са зависими: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- Следната изчислителна формула е валидна за дисперсия:
D(X)=M(X 2)-(M(X)) 2
Пример. Известни са математическите очаквания и дисперсиите на две независими случайни променливи X и Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Намерете математическото очакване и дисперсията на случайната променлива Z=9X-8Y+7.
Решение. Въз основа на свойствата на математическото очакване: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Въз основа на свойствата на дисперсията: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Алгоритъм за изчисляване на математическото очакване
Свойства на дискретни случайни променливи: всичките им стойности могат да бъдат преномерирани с естествени числа; Присвоете на всяка стойност ненулева вероятност.- Умножаваме двойките една по една: x i по p i .
- Добавете произведението на всяка двойка x i p i .
Например за n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Пример №1.
| x i | 1 | 3 | 4 | 7 | 9 |
| p i | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Намираме математическото очакване по формулата m = ∑x i p i .
Очакване M[X].
M[x] = 1*0,1 + 3*0,2 + 4*0,1 + 7*0,3 + 9*0,3 = 5,9
Намираме дисперсията с помощта на формулата d = ∑x 2 i p i - M[x] 2 .
Дисперсия D[X].
D[X] = 1 2 *0,1 + 3 2 *0,2 + 4 2 *0,1 + 7 2 *0,3 + 9 2 *0,3 - 5,9 2 = 7,69
Стандартно отклонение σ(x).
σ = sqrt(D[X]) = sqrt(7,69) = 2,78
Пример №2. Дискретна случайна променлива има следната серия на разпределение:
| х | -10 | -5 | 0 | 5 | 10 |
| Р | А | 0,32 | 2а | 0,41 | 0,03 |
Решение. Стойността на a се намира от връзката: Σp i = 1
Σp i = a + 0,32 + 2 a + 0,41 + 0,03 = 0,76 + 3 a = 1
0,76 + 3 a = 1 или 0,24=3 a , откъдето a = 0,08
Пример №3. Определете закона за разпределение на дискретна случайна променлива, ако нейната дисперсия е известна и x 1
р 1 =0.3; р2=0.3; р3 =0.1; р4 =0,3
d(x)=12,96
Решение.
Тук трябва да създадете формула за намиране на дисперсията d(x):
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
където очакването m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
За нашите данни
m(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0,1x 3) 2
или -9/100 (x 2 -20x+96)=0
Съответно трябва да намерим корените на уравнението и ще има два от тях.
x 3 =8, x 3 =12
Изберете този, който отговаря на условието x 1
Закон за разпределение на дискретна случайна величина
х 1 =6; х 2 =9; х 3 =12; х 4 =15
р 1 =0.3; р2=0.3; р3 =0.1; р4 =0,3
Където σ 2 j е вътрешногруповата дисперсия на j-та група.
За негрупирани данни остатъчна дисперсия– мярка за точност на приближението, т.е. приближаване на регресионната линия към оригиналните данни: 
където y(t) е прогнозата, използваща уравнението на тенденцията; y t – начален динамичен ред; n – брой точки; p – брой на коефициентите на регресионното уравнение (брой на обяснителните променливи).
В този пример се нарича безпристрастен оценител на дисперсията.
Пример №1. Разпределението на работниците от три предприятия от една асоциация според тарифните категории се характеризира със следните данни:
| Тарифна категория на работника | Броят на работниците в предприятието | ||
| предприятие 1 | предприятие 2 | предприятие 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Определете:
1. отклонение за всяко предприятие (вътрешногрупови отклонения);
2. средната стойност на вътрешногруповите дисперсии;
3. междугрупова дисперсия;
4. обща дисперсия.
Решение.
Преди да започнете да решавате проблема, е необходимо да разберете коя функция е ефективна и коя факторна. В разглеждания пример резултатният признак е „Тарифна категория“, а факторният признак е „Номер (име) на предприятието“.
След това имаме три групи (предприятия), за които е необходимо да се изчислят средните групови и вътрешногрупови дисперсии:
| Компания | Средна група, | Дисперсия в рамките на групата, |
| 1 | 4 | 1,8 |
Средната стойност на дисперсиите в рамките на групата ( остатъчна дисперсия) ще се изчисли по формулата:
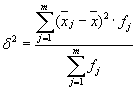
където можете да изчислите:
или:
Тогава:
Общата дисперсия ще бъде равна на: s 2 = 1,6 + 0 = 1,6.
Общата дисперсия може също да се изчисли с помощта на една от следните две формули:
При решаването на практически проблеми често се налага да се справяте с функция, която приема само две алтернативни стойности. В този случай не говорим за тежестта на определена стойност на признак, а за неговия дял в съвкупността. Ако делът на единиците от съвкупността, притежаващи изследваната характеристика, се обозначава с „ Р", а тези, които нямат - през " р", тогава дисперсията може да се изчисли по формулата:
s 2 = p×q
Пример №2. Въз основа на производствените данни на шестима работници в екип, определете междугруповата вариация и оценете влиянието на работната смяна върху тяхната производителност на труда, ако общата вариация е 12,2.
| Работник в екип бр. | Работна продукция, бр. | |
| в първа смяна | във втора смяна | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Решение. Изходни данни
| х | е 1 | е 2 | е 3 | е 4 | е 5 | е 6 | Обща сума |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Обща сума | 31 | 33 | 37 | 37 | 40 | 38 |
След това имаме 6 групи, за които е необходимо да се изчисли груповата средна стойност и вътрешногруповите дисперсии.
1. Намерете средните стойности на всяка група.
2. Намерете средния квадрат на всяка група.
Нека обобщим резултатите от изчислението в таблица:
| Номер на групата | Групово средно | Дисперсия в рамките на групата |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Дисперсия в рамките на групатахарактеризира промяната (вариацията) на изследваната (резултатна) характеристика в рамките на група под въздействието на всички фактори върху нея, с изключение на фактора, който е в основата на групирането:
Изчисляваме средната стойност на вътрешногруповите дисперсии по формулата:
4. Междугрупова дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) характеристика под въздействието на фактор (факторна характеристика), който формира основата на групата.
Ние определяме междугруповата вариация като:
Където
Тогава
Обща дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) характеристика под въздействието на всички фактори (факторни характеристики) без изключение. Според условията на задачата то е равно на 12,2.
Емпирична корелационна връзкаизмерва каква част от общата променливост на резултантната характеристика е причинена от изследвания фактор. Това е съотношението на факторната вариация към общата вариация:
Ние дефинираме емпиричната корелационна връзка:
Връзките между характеристиките могат да бъдат слаби и силни (близки). Техните критерии се оценяват по скалата на Chaddock:
0,1 0,3 0,5 0,7 0,9 В нашия пример връзката между признака Y и фактор X е слаба
Коефициент на определяне.
Нека определим коефициента на детерминация:
По този начин 0,67% от вариацията се дължи на разликите между признаците, а 99,37% се дължи на други фактори.
Заключение: в този случай продукцията на работниците не зависи от работата на конкретна смяна, т.е. влиянието на работната смяна върху тяхната производителност на труда не е значително и се дължи на други фактори.
Пример №3. Въз основа на данните за средната работна заплата и квадрата на отклоненията от нейната стойност за две групи работници, намерете общата дисперсия, като приложите правилото за събиране на дисперсии:
Решение:Средна стойност на дисперсиите в рамките на групата
Ние определяме междугруповата вариация като:
Общата дисперсия ще бъде: 480 + 13824 = 14304