В тази тема ще говорим подробно за изчисляването на неопределени интеграли с помощта на така наречената „формула за интегриране по части“. Ще ни трябва таблица с неопределени интеграли и таблица с производни. В първата част ще бъдат разгледани стандартни примери, които се срещат най-вече в стандартните изчисления и тестове. | Повече ▼ сложни примериразгледани във втората част.

Формулировката на проблема в стандартния случай е следната. Да кажем, че под интеграла имаме две функции от различен характер : полином и тригонометрична функция, полином и логаритъм, полином и обратна тригонометрична функция и т.н. В тази ситуация е изгодно да се отдели една функция от друга. Грубо казано, има смисъл интеграндът да се раздели на части - и да се работи с всяка част отделно. Оттук и името: „интеграция по части“. Приложението на този метод се основава на следната теорема:

Нека функциите $u(x)$ и $v(x)$ са диференцируеми на някакъв интервал и на този интервал съществува интеграл $\int v \; du$. Тогава на същия интервал съществува интеграл $\int u \; dv$ и е вярно следното равенство:

\begin(equation) \int u \; dv=u\cdot v-\int v\; du \край (уравнение)

Формула (1) се нарича „формула за интегриране по части“. Понякога, когато прилагат горната теорема, те говорят за използването на „метода на интегриране по части“. Същността на този метод ще бъде важна за нас, която ще разгледаме с примери. Има няколко стандартни случая, в които формула (1) очевидно е приложима. Именно тези случаи ще станат тема на тази страница. Нека $P_n(x)$ - n-ти полиномстепени. Нека въведем две правила:

Правило #1

За интеграли от формата $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$, $\ int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ вземаме $dv=P_n(x)dx$.

Правило #2

За интеграли от вида $\int P_n(x) a^x \;dx$ ($a$ е някакво положително число), $\int P_n(x) \sin x \;dx$, $\int P_n(x ) \ cos x \;dx$, $\int P_n(x)ch x \;dx$, $\int P_n(x) sh x \;dx$ вземаме $u=P_n(x)$.

Нека веднага да отбележа, че горните записи не трябва да се приемат буквално. Например, в интеграли от формата $\int P_n(x) \ln x \;dx$ не е задължително да има точно $\ln x$. Както $\ln 5x$, така и $\ln (10x^2+14x-5)$ могат да бъдат разположени там. Тези. нотацията $\ln x$ трябва да се приема като вид обобщение.

Още нещо. Случва се формулата за интегриране по части да се приложи няколко пъти. Нека поговорим за това по-подробно в примери № 4 и № 5. Сега нека да преминем директно към решаването на типични проблеми. Решаването на задачи, чието ниво е малко по-високо от стандартното, се разглежда във втората част.

Пример №1

Намерете $\int (3x+4) \cos (2x-1) \; dx$.

Под интеграла е полиномът $3x+4$ и тригонометричната функция $\cos (2x-1)$. Това е класически случай за прилагане на формулата, така че нека вземем дадения интеграл по части. Формулата изисква интегралът $\int (3x+4) \cos (2x-1)\; dx$ беше представен във формата $\int u\; dv$. Трябва да изберем изрази за $u$ и за $dv$. Можем да приемем $3x+4$ като $u$, тогава $dv=\cos (2x-1)dx$. Можем да вземем $u=\cos (2x-1)$, тогава $dv=(3x+4)dx$. Да направя правилен изборнека се обърнем към . Даден интеграл $\int (3x+4) \cos (2x-1)\; dx$ попада под формата $\int P_n(x) \cos x \;dx$ (полиномът $P_n(x)$ в нашия интеграл има формата $3x+4$). Според, трябва да изберете $u=P_n(x)$, т.е. в нашия случай $u=3x+4$. Тъй като $u=3x+4$, тогава $dv=\cos(2x-1)dx$.

Обаче простото избиране на $u$ и $dv$ не е достатъчно. Ще ни трябват и стойностите на $du$ и $v$. Тъй като $u=3x+4$, тогава:

$$ du=d(3x+4)=(3x+4)"dx=3dx.$$

Сега нека разгледаме функцията $v$. Тъй като $dv=\cos(2x-1)dx$, то според дефиницията на неопределения интеграл имаме: $ v=\int \cos(2x-1)\; dx$. За да намерим необходимия интеграл, прилагаме следното към диференциалния знак:

$$ v=\int \cos(2x-1)\; dx=\frac(1)(2)\cdot \int \cos(2x-1)d(2x-1)=\frac(1)(2)\cdot \sin(2x-1)+C=\frac (\sin(2x-1))(2)+C. $$

Все пак не ни трябва всичко безкрайно множествофункции $v$, която се описва с формулата $\frac(\sin(2x-1))(2)+C$. Имаме нужда от малко единфункция от този набор. За да получите необходимата функция, трябва да замените някакво число вместо $C$. Най-лесният начин, разбира се, е да се замени $C=0$, като по този начин се получи $v=\frac(\sin(2x-1))(2)$.

И така, нека съберем всичко по-горе заедно. Имаме: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac(\sin(2x-1))(2)$. Замествайки всичко това в правилната странаще имаме формули:

$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx. $$

Всъщност всичко, което остава, е да се намери $\int\frac(\sin(2x-1))(2)\cdot 3dx$. Вземайки константата (т.е. $\frac(3)(2)$) извън интегралния знак и прилагайки метода за въвеждането й под диференциалния знак, получаваме:

$$ (3x+4)\cdot \frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx= \frac((3x+ 4 )\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx= \\ =\frac((3x+4)\cdot \ sin(2x-1))(2)-\frac(3)(4)\int \sin(2x-1) \;d(2x-1)= \frac((3x+4)\cdot\sin ( 2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C=\\ =\frac((3x+4)\cdot\sin(2x - 1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C. $$

И така $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$. В съкратена форма процесът на решение е написан, както следва:

$$ \int (3x+4) \cos (2x-1) \; dx=\ляво | \begin(aligned) & u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac(\sin(2x-1))(2). \end(aligned) \right |=\\ =(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2) \cdot 3dx= \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx=\\ = \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C= \frac((3x +4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot\cos (2x-1)+C. $$

Неопределеният интеграл е намерен по части; остава само да се запише отговорът.

Отговор: $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$.

Вярвам, че тук има въпрос, така че ще се опитам да го формулирам и да дам отговор.

Защо взехме точно $u=3x+4$ и $dv=\cos(2x-1)dx$? Да, интегралът е решен. Но може би ако вземем $u=\cos (2x-1)$ и $dv=(3x+4)dx$ интегралът също ще бъде намерен!

Не, ако вземем $u=\cos (2x-1)$ и $dv=(3x+4)dx$, тогава нищо добро няма да излезе от това - интегралът няма да бъде опростен. Преценете сами: ако $u=\cos(2x-1)$, тогава $du=(\cos(2x-1))"dx=-2\sin(2x-1)dx$. Освен това, тъй като $ dv =(3x+4)dx$, тогава:

$$ v=\int (3x+4) \; dx=\frac(3x^2)(2)+4x+C.$$

Като вземем $C=0$, получаваме $v=\frac(3x^2)(2)+4x$. Нека сега заместим намерените стойности на $u$, $du$, $v$ и $dv$ във формулата:

$$ \int (3x+4) \cos (2x-1) \; dx=\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) - \int \left(\frac(3x^2)(2)+4x \right) \cdot (-2\sin(2x-1)dx)=\\ =\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) +2\cdot\ int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx $$

И до какво стигнахме? Стигнахме до интеграла $\int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx$, който очевидно е по-сложен от оригиналния интеграл $\int (3x+4) \cos (2x-1) \; dx$. Това предполага, че изборът на $u$ и $dv$ е направен лошо. След прилагане на формулата за интегриране по части, полученият интеграл трябва да е по-прост от оригиналния. Когато намираме неопределения интеграл по части, трябва да го опростим, а не да го усложним, така че ако след прилагане на формула (1) интегралът стане по-сложен, тогава изборът на $u$ и $dv$ е направен неправилно.

Пример №2

Намерете $\int (3x^4+4x-1) \ln 5x \; dx$.

Под интеграла има полином (т.е. $3x^4+4x-1$) и $\ln 5x$. Този случай попада под , така че нека вземем интеграла по части. Даденият интеграл има същата структура като интеграла $\int P_n(x) \ln x\; dx$. Отново, както в пример № 1, трябва да изберем част от интегранта $(3x^4+4x-1) \ln 5x \; dx$ като $u$ и част като $dv$. Според , трябва да изберете $dv=P_n(x)dx$, т.е. в нашия случай $dv=(3x^4+4x-1)dx$. Ако от израза $(3x^4+4x-1) \ln 5x \; dx$ "премахване" $dv=(3x^4+4x-1)dx$, тогава $\ln 5x$ ще остане - това ще бъде функцията $u$. И така, $dv=(3x^4+4x-1)dx$, $u=\ln 5x$. За да приложим формулата, имаме нужда също от $du$ и $v$. Тъй като $u=\ln 5x$, тогава:

$$ du=d(\ln 5x)=(\ln 5x)"dx=\frac(1)(5x)\cdot 5 dx=\frac(1)(x)dx. $$

Сега нека намерим функцията $v$. Тъй като $dv=(3x^4+4x-1)dx$, тогава:

$$ v=\int(3x^4+4x-1)\; dx=\frac(3x^5)(5)+2x^2-x+C. $$

От целия намерен безкраен набор от функции $\frac(3x^5)(5)+2x^2-x+C$ трябва да изберем една. И най-лесният начин да направите това е като вземете $C=0$, т.е. $v=\frac(3x^5)(5)+2x^2-x$. Всичко е готово за прилагане на формулата. Нека заместим стойностите $u=\ln 5x$, $du=\frac(1)(x)dx$, $v=\frac(3x^5)(5)+2x^2-x$ и $dv=(3x^4+4x-1)dx$ ще имаме:

$$ \int (3x^4+4x-1) \ln 5x \; dx=\ляво | \begin(aligned) & u=\ln 5x; \; du=\frac(1)(x)dx.\\ & dv=(3x^4+4x-1)dx; \; v=\frac(3x^5)(5)+2x^2-x. \end(aligned) \right |=\\ =\ln 5x \cdot \left (\frac(3x^5)(5)+2x^2-x \right)-\int \left (\frac(3x^ 5)(5)+2x^2-x \right)\cdot \frac(1)(x)dx=\\ =\left (\frac(3x^5)(5)+2x^2-x \right )\cdot\ln 5x -\int \left (\frac(3x^4)(5)+2x-1 \right)dx=\\ =\left (\frac(3x^5)(5)+2x^ 2-x \вдясно)\cdot\ln 5x - \вляво (\frac(3x^5)(25)+x^2-x \вдясно)+C=\\ =\вляво (\frac(3x^5) (5)+2x^2-x \надясно)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C. $$

Отговор: $\int (3x^4+4x-1) \ln 5x \; dx=\left (\frac(3x^5)(5)+2x^2-x \right)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C$.

Пример №3

Намерете $\int \arccos x\; dx$.

Този интеграл има структурата $\int P_n(x) \arccos x \;dx$, попадаща под . Разбирам, че веднага ще възникне резонен въпрос: „къде в дадения интеграл $\int\arccos x \; dx$ са скрили полинома $P_n(x)$ Там няма полином, а само аркосинус и това е! ” Всъщност обаче не само арккосинусът се намира под интеграла. Ще представя интеграла $\int arccos x\; dx$ в тази форма: $\int 1\cdot\arccos x \; dx$. Съгласете се, че умножаването по едно няма да промени интегранта. Тази единица е $P_n(x)$. Тези. $dv=1\cdot dx=dx$. И като $u$ (според ) приемаме $\arccos x$, т.е. $u=\arccos x$. Намираме стойностите $du$ и $v$, които участват във формулата, по същия начин, както в предишните примери:

$$ du=(\arccos x)"dx=-\frac(1)(\sqrt(1-x^2))dx;\\ v=\int 1\; dx=x+C. $$

Както в предишните примери, приемайки $C=0$, получаваме $v=x$. Замествайки всички намерени параметри във формулата, ще имаме следното:

$$ \int \arccos x \; dx=\ляво | \begin(aligned) & u=\arccos x; \; du=-\frac(1)(\sqrt(1-x^2))dx.\\ & dv=dx; \; v=x. \end(aligned) \right |=\\ =\arccos x \cdot x-\int x\cdot \left(-\frac(1)(\sqrt(1-x^2))dx \right)= \ arccos x \cdot x+\int \frac(xdx)(\sqrt(1-x^2))=\\ =x\cdot\arccos x-\frac(1)(2)\cdot\int (1-x ^2)^(-\frac(1)(2))d(1-x^2)= =x\cdot\arccos x-\frac(1)(2)\cdot\frac((1-x^ 2)^(\frac(1)(2)))(\frac(1)(2))+C=\\ =x\cdot\arccos x-\sqrt(1-x^2)+C. $$

Отговор: $\int\arccos x\; dx=x\cdot\arccos x-\sqrt(1-x^2)+C$.

Пример №4

Намерете $\int (3x^2+x) e^(7x) \; dx$.

В този пример формулата за интегриране по части ще трябва да се приложи два пъти. Интеграл $\int (3x^2+x) e^(7x) \; dx$ има структурата $\int P_n(x) a^x \;dx$. В нашия случай $P_n(x)=3x^2+x$, $a=e$. Според имаме: $u=3x^2+x$. Съответно $dv=e^(7x)dx$.

$$ du=(3x^2+x)"=(6x+1)dx;\\ v=\int e^(7x)\;dx=\frac(1)(7)\cdot \int e^( 7x)\;d(7x)=\frac(1)(7)\cdot e^(7x)+C=\frac(e^(7x))(7)+C $$.

Отново, както в предишните примери, приемайки $C=0$, имаме: $v=\frac(e^(7x))(7)$.

$$ \int (3x^2+x) e^(7x) \; dx=\ляво | \begin(aligned) & u=3x^2+x; \; du=(6x+1)dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(aligned) \right |=\\ =(3x^2+x)\cdot\frac(e^(7x))(7)-\int \frac(e^(7x))(7)\cdot (6x+1)dx= \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\ ;dx. $$

Стигнахме до интеграла $\int (6x+1) e^(7x)\;dx$, който отново трябва да се вземе на части. Като вземем $u=6x+1$ и $dv=e^(7x)dx$ имаме:

$$ \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\;dx=\left | \begin(aligned) & u=6x+1; \; du=6dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(подравнено) \right |=\\ =\frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \left ((6x+1) \cdot\frac(e^(7x))(7) - \int\frac(e^(7x))(7)\cdot 6\;dx \right)=\\ =\frac((3x^2+ x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49)\cdot\int\ e^(7x)\; dx=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49 )\cdot\frac(e^(7x))(7)+C=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e ^(7x))(49) +\frac(6\; e^(7x))(343)+C. $$

Полученият отговор може да бъде опростен чрез отваряне на скобите и пренареждане на термините:

$$ \frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6\; e^(7x) ))(343)+C=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+ ° С. $$

Отговор: $\int (3x^2+x) e^(7x) \; dx=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+C$.

Пример №5

Намерете $\int (x^2+5)\sin(3x+1) \; dx$.

Тук, както и в предишния пример, интегрирането по части се прилага два пъти. Подробни обяснения бяха дадени по-рано, така че ще дам само решението:

$$ \int (x^2+5)\sin(3x+1) \; dx=\ляво | \begin(aligned) & u=x^2+5; \; du=2xdx.\\ & dv=\sin(3x+1)dx; \; v=-\frac(\cos(3x+1))(3). \end(aligned) \right |=\\ =(x^2+5)\cdot \left(-\frac(\cos(3x+1))(3) \right)-\int\left(-\ frac(\cos(3x+1))(3) \right)\cdot 2xdx=\\ = -\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac (2)(3)\int x\cos(3x+1)dx= \left | \begin(aligned) & u=x; \; du=dx.\\ & dv=\cos(3x+1)dx; \; v=\frac(\sin(3x+1))(3). \end(aligned) \right |=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2)(3)\cdot \left( x\cdot\frac(\sin(3x+1))(3)-\int\frac(\sin(3x+1))(3)dx \right)=\\ =-\frac((x^2 +5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(2)(9)\cdot\int\sin(3x+ 1) )dx=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac ( 2)(9)\cdot \left(-\frac(\cos(3x+1))(3)\right)+C=\\ = -\frac((x^2+5)\cdot\cos ( 3x+1))(3) +\frac(2x\sin(3x+1))(9)+\frac(2\cos(3x+1))(27)+C=\\ =-\frac ( x^2\cdot\cos(3x+1))(3)-\frac(5\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9 ) +\frac(2\cos(3x+1))(27)+C=\\ =-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin ( 3x+1))(9)-\frac(43\cos(3x+1))(27)+C. $$

Отговор: $\int (x^2+5)\sin(3x+1) \; dx=-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(43\cos(3x+1) )(27)+C$.

В

Решаването на интеграли е лесна задача, но само за малцина избрани. Тази статия е за тези, които искат да се научат да разбират интегралите, но не знаят нищо или почти нищо за тях. Интеграл... Защо е необходим? Как да го изчислим? Какво представляват определени и неопределени интеграли? Ако единствената употреба, която знаете за интеграла, е да използвате кука за плетене на една кука, оформена като интегрална икона, за да извадите нещо полезно от труднодостъпни места, тогава добре дошли! Разберете как се решават интеграли и защо не можете без това.

Ние изучаваме понятието "интеграл"

Интеграцията беше известна още през Древен Египет. Разбира се, не в модерна форма, но все пак. Оттогава математиците са написали много книги по тази тема. Особено се отличиха Нютон И Лайбниц , но същността на нещата не се е променила. Как да разберем интегралите от нулата? Няма начин! За да разберете тази тема, все пак ще ви трябват основни познания за основите на математическия анализ. Вече имаме информация за , необходима за разбирането на интегралите, в нашия блог.

Неопределен интеграл

Нека имаме някаква функция f(x) .

Неопределена интегрална функция f(x) тази функция се нарича F(x) , чиято производна е равна на функцията f(x) .

С други думи, интегралът е обратно производно или антипроизводно. Между другото, прочетете как в нашата статия.

Антипроизводното съществува за всички непрекъснати функции. Също така към антипроизводното често се добавя постоянен знак, тъй като производните на функции, които се различават по константа, съвпадат. Процесът на намиране на интеграла се нарича интегриране.

Прост пример:

За да не пресмятаме постоянно противопроизводни елементарни функции, удобно е да ги обобщите в таблица и да използвате готови стойности:

Определен интеграл

Когато се занимаваме с концепцията за интеграл, имаме работа с безкрайно малки количества. Интегралът ще помогне да се изчисли площта на фигура, масата на нееднородно тяло, изминатото разстояние по време на неравномерно движение и много други. Трябва да се помни, че интегралът е безкрайна сума голямо количествобезкрайно малки термини.

Като пример, представете си графика на някаква функция. Как да намерим площта на фигура, ограничена от графиката на функция?

С помощта на интеграл! Нека разделим криволинейния трапец, ограничен от координатните оси и графиката на функцията, на безкрайно малки сегменти. По този начин фигурата ще бъде разделена на тънки колони. Сумата от площите на колоните ще бъде площта на трапеца. Но не забравяйте, че такова изчисление ще даде приблизителен резултат. Въпреки това, колкото по-малки и по-тесни са сегментите, толкова по-точно ще бъде изчислението. Ако ги намалим до такава степен, че дължината клони към нула, тогава сумата от площите на сегментите ще клони към площта на фигурата. Това е определен интеграл, който се записва така:

Точки a и b се наричат ​​граници на интегриране.

Бари Алибасов и групата "Интеграл"

Между другото! За нашите читатели вече има 10% отстъпка от

Правила за изчисляване на интеграли за манекени

Свойства на неопределения интеграл

Как да решим неопределен интеграл? Тук ще разгледаме имотите определен интеграл, което ще бъде полезно при решаване на примери.

• Производната на интеграла е равна на интеграла:

• Константата може да бъде извадена от знака за интеграл:

• Интегралът от сбора е равен на сбора от интегралите. Това важи и за разликата:

Свойства на определен интеграл

• Линейност:

• Знакът на интеграла се променя, ако границите на интегриране се разменят:

• При всякаквиточки а, bИ с:

Вече разбрахме, че определен интеграл е границата на сумата. Но как да получите конкретна стойност при решаване на пример? За това има формулата на Нютон-Лайбниц:

Примери за решаване на интеграли

По-долу ще разгледаме няколко примера за намиране на неопределени интеграли. Предлагаме ви сами да разберете тънкостите на решението и ако нещо не е ясно, задайте въпроси в коментарите.

За да затвърдите материала, изгледайте видео как се решават интеграли на практика. Не се отчайвайте, ако интегралът не е даден веднага. Свържете се с професионален студентски сервиз и всяка тройна или криволинейни интегралина затворена повърхност ще можете да го направите.

Извиква се следната формула формула за интегриране по части в неопределен интеграл:

За да се приложи формулата за интегриране по части, интегралната функция трябва да бъде разделена на два фактора. Един от тях е означен с u, а остатъкът се отнася за втория фактор и се означава с дв. След това чрез диференциране намираме дуи интеграция – функция v. В същото време за u дв- такава част от интегранта, която може лесно да се интегрира.

Кога е полезно да се използва методът на интегриране по части? Тогава когато интеграндът съдържа :

1) - логаритмични функции, както и обратни тригонометрични функции(с префикса "дъга"), тогава, въз основа на дългогодишен опит на интегриране по части, тези функции се означават с u;

2) , , - синус, косинус и експонента, умножени по П(х) е произволен полином от x, тогава тези функции се означават с дв, а полиномът е през u;

3) , , , , в този случай интегрирането по части се прилага два пъти.

Нека обясним стойността на метода на интегриране по части, използвайки примера на първия случай. Нека изразът под знака за интеграл съдържа логаритмична функция (това ще бъде пример 1). Чрез използването на интегриране по части такъв интеграл се свежда до изчисляване на интеграла само на алгебрични функции (най-често полином), т.е. не съдържа логаритмична или обратна тригонометрична функция. Използване на формулата за интегриране по части, дадена в самото начало на урока

получаваме в първия член (без интеграл) логаритмична функция, а във втория член (под знака на интеграла) функция, която не съдържа логаритъм. Интегралът на алгебрична функция е много по-прост от интеграла, под чийто знак се намира логаритмична или обратна тригонометрична функция отделно или заедно с алгебричен фактор.

По този начин, използвайки интегриране по части формули интегрирането не се извършва веднага: намирането на даден интеграл се свежда до намиране на друг. Смисълът на формулата за интегриране по части е, че в резултат на нейното прилагане новият интеграл се оказва табличен или поне става по-опростен от първоначалния.

Методът на интегриране по части се основава на използването на формулата за диференциране на продукта на две функции:

тогава може да се запише във формата

който беше даден в самото начало на урока.

При намиране чрез интегриране на функцията vза него има безкраен набор антипроизводни функции. За да приложите формулата за интегриране по части, можете да вземете всяка от тях и следователно тази, която съответства на произволна константа СЪС, равно на нула. Следователно при намиране на функцията vпроизволна константа СЪСне трябва да се въвежда.

Методът на интегриране по части има много специално приложение: той може да се използва за извеждане на рекурентни формули за намиране на първоизводни функции, когато е необходимо да се намали степента на функциите под интегралния знак. Намаляването на степента е необходимо, когато няма таблични интеграли за, например, функции като синуси и косинуси до степени, по-големи от секундата и техните произведения. Рекурентна формула е формула за намиране на следващия член на последователност чрез предишния член. За посочените случаи целта се постига с последователно понижаване на степента. И така, ако интеграндът е синус на четвърта степен от х, тогава чрез интегриране по части можете да намерите формула за интеграла на синус на трета степен и т.н. Последният параграф от този урок е посветен на описаната задача.

Прилагане на интеграция по части заедно

Пример 1. Намерете неопределения интеграл, като използвате метода на интегриране по части:

Решение. В израза на интегранд - логаритъма, който, както вече знаем, може разумно да бъде обозначен с u. Вярваме, че ,.

Намираме (както вече беше споменато в обяснението за теоретичната справка, веднага получаваме логаритмична функция в първия член (без интеграл) и функция, която не съдържа логаритъм във втория член (под интегралния знак):

И пак логаритъм...

Пример 2.Намерете неопределения интеграл:

Решение. Позволявам , .

Логаритъмът присъства в квадрата. Това означава, че трябва да се разграничи като сложна функция. Намираме
,
.

Отново намираме втория интеграл по части и получаваме вече споменатото предимство (в първия член (без интеграла) има логаритмична функция, а във втория член (под знака на интеграла) има функция, която не съдържа логаритъм).

Намираме първоначалния интеграл:

Пример 3.

Решение. Арктангенсът, подобно на логаритъма, е по-добре да се означава с u. Така че нека,.

Тогава ,
.

Прилагайки формулата за интегриране по части, получаваме:

Намираме втория интеграл чрез промяна на променлива.

Връщане към променливата х, получаваме

.

Намираме първоначалния интеграл:

.

Пример 4. Намерете неопределения интеграл, като използвате метода на интегриране по части:

Решение. По-добре е степента да се обозначи с дв. Разделяме интегранта на два фактора. Вярвайки в това

Пример 5. Намерете неопределения интеграл, като използвате метода на интегриране по части:

.

Решение. Позволявам , . Тогава , .

Използвайки формулата за интегриране по части (1), намираме:

Пример 6.Намерете неопределения интеграл чрез интегриране по части:

Решение. Синусът, подобно на експоненциала, може удобно да се обозначи с дв. Позволявам , .

Използвайки формулата за интегриране по части, намираме:

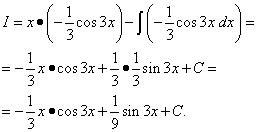
Отново прилагаме интегриране по части заедно

Пример 10.Намерете неопределения интеграл чрез интегриране по части:

.

Решение. Както във всички подобни случаи, удобно е косинусът да се обозначи с дв. Означаваме , .

Тогава , .

Използвайки формулата за интегриране по части, получаваме:

Също така прилагаме интегриране по части към втория член. Означаваме , .

Използвайки тези обозначения, ние интегрираме споменатия термин:

Сега намираме необходимия интеграл:

Сред интегралите, които могат да се решават чрез метода на интегриране по части, има и такива, които не са включени в нито една от трите групи, посочени в теоретичната част, за които е известно от практиката, че е по-добре да се означават с u, и през какво дв. Следователно в тези случаи трябва да използвате съображението за удобство, също дадено в параграфа „Същността на метода на интегриране по части“: за uтрябва да се вземе част от интегранта, която не става много по-сложна по време на диференцирането, но дв- такава част от интегранта, която може лесно да се интегрира. Последният пример от този урок е решението на точно такъв интеграл.

Формулата за интегриране по части изглежда така:
.

Методът на интегриране по части се състои в прилагането на тази формула. При практическо приложениеСтрува си да се отбележи, че u и v са функции на интеграционната променлива. Нека променливата за интегриране бъде обозначена като x (символът след диференциалния знак d в края на интегралната нотация). Тогава u и v са функции на x: u(x) и v(x) .
Тогава
, .
А формулата за интегриране по части приема формата:
.

Тоест функцията интегранд трябва да се състои от произведението на две функции:
,
едното от които означаваме като u: g(x) = u, а за другото трябва да се изчисли интегралът (по-точно трябва да се намери първоизводната):
, тогава dv = f(x) dx .

В някои случаи f(x) = 1 . Тоест в интеграла
,
можем да поставим g(x) = u, x = v.

Резюме

И така, в този метод, формулата за интегриране по части си струва да запомните и приложите в две форми:
;
.

Интеграли, изчислени чрез интегриране по части

Интеграли, съдържащи логаритми и обратни тригонометрични (хиперболични) функции

Интегралите, съдържащи логаритми и обратни тригонометрични или хиперболични функции, често се интегрират по части. В този случай частта, която съдържа логаритъм или обратни тригонометрични (хиперболични) функции, се означава с u, а останалата част с dv.

Ето примери за такива интеграли, които се изчисляват по метода на интегриране по части:
, , , , , , .

Интеграли, съдържащи произведението на полином и sin x, cos x или e x

С помощта на формулата за интегриране по части се намират интеграли от вида:
, , ,
където P(x) е полином от x. При интегриране полиномът P(x) се означава с u и e ax dx, cos ax dxили sin ax dx- чрез dv.

Ето примери за такива интеграли:
, , .

Примери за изчисляване на интеграли с помощта на метода на интегриране по части

Примери за интеграли, съдържащи логаритми и обратни тригонометрични функции

Пример

Изчислете интеграла:

Подробно решение

Тук интегралната функция съдържа логаритъм. Правене на замествания
u = в х,
dv = x 2 dx.
Тогава
,
.

Изчисляваме оставащия интеграл:
.
Тогава
.
В края на изчисленията е необходимо да добавите константата C, тъй като неопределеният интеграл е множеството от всички първоизводни. Може да се добави и в междинни изчисления, но това само би затрупало изчисленията.

По-кратко решение

Можете да представите решението в по-кратък вариант. За да направите това, не е необходимо да правите замествания с u и v, но можете да групирате факторите и да приложите формулата за интегриране по части във втората форма.

.

Отговор

Примери за интеграли, съдържащи произведението на полином и sin x, cos x или ex

Пример

Изчислете интеграла:
.

Решение

Нека въведем показателя под диференциалния знак:
e - x dx = - e - x d(-x) = - d(e - x).

Нека интегрираме по части.
.
Използваме и метода на интегриране по части.
.
.
.
Най-накрая имаме.

Извиква се функция F(x), диференцируема в даден интервал X първоизводна на функцията f(x) или интеграла на f(x), ако за всяко x ∈X е валидно следното равенство:

F " (x) = f(x). (8.1)

Намирането на всички първоизводни за дадена функция се нарича нейна интеграция. Неопределена интегрална функция f(x) на даден интервал X е множеството от всички първообразни функции за функцията f(x); обозначаване -

Ако F(x) е някакво първообразно за функцията f(x), тогава ∫ f(x)dx = F(x) + C, (8.2)

където C е произволна константа.

Таблица на интегралите

Директно от дефиницията получаваме основните свойства на неопределения интеграл и списък от таблични интеграли:

1) d∫f(x)dx=f(x)

2) ∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Списък на табличните интеграли

1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = арктан x + C

8. = arcsin x + C

10. = - ctg x + C

Променлива замяна

За да интегрирате много функции, използвайте метода за заместване на променливи или замествания,което ви позволява да намалите интегралите до таблична форма.

Ако функцията f(z) е непрекъсната върху [α,β], функцията z =g(x) има непрекъсната производна и α ≤ g(x) ≤ β, тогава

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Освен това, след интегриране от дясната страна, трябва да се направи заместването z=g(x).

За да го докажете, достатъчно е да напишете оригиналния интеграл във формата:

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Например:

Метод на интегриране по части

Нека u = f(x) и v = g(x) са функции, които имат непрекъснато . Тогава, според работата,

d(uv))= udv + vdu или udv = d(uv) - vdu.

За израза d(uv) антипроизводното очевидно ще бъде uv, така че формулата е валидна:

∫ udv = uv - ∫ vdu (8.4.)

Тази формула изразява правилото интеграция по части. Това води интегрирането на израза udv=uv"dx до интегрирането на израза vdu=vu"dx.

Нека, например, искате да намерите ∫xcosx dx. Нека поставим u = x, dv = cosxdx, така че du=dx, v=sinx. Тогава

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Правилото за интегриране по части има по-ограничен обхват от заместването на променливи. Но има цели класове интеграли, напр.

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и други, които се изчисляват точно с помощта на интегриране по части.

Определен интеграл

Концепцията за определен интеграл се въвежда по следния начин. Нека функция f(x) е дефинирана на интервал. Нека разделим сегмента [a,b] на нчасти по точки a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i = x i - x i-1. Извиква се сума от формата f(ξ i)Δ x i интегрална сума, а неговата граница при λ = maxΔx i → 0, ако съществува и е крайна, се нарича определен интегралфункции f(x) на апреди bи се обозначава:

F(ξ i)Δx i (8.5).

Функцията f(x) в този случай се извиква интегрируеми на интервала, се наричат ​​числата a и b долна и горна граница на интеграла.

За определен интеграл са валидни следните свойства:

4), (k = const, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

Последното свойство се нарича теорема за средната стойност.

Нека f(x) е непрекъснато върху . Тогава на този сегмент има неопределен интеграл

∫f(x)dx = F(x) + C

и се провежда Формула на Нютон-Лайбниц, свързващ определения интеграл с неопределения интеграл:

F(b) - F(a). (8,6)

Геометрична интерпретация: определеният интеграл е площта на криволинейния трапец, ограничен отгоре от кривата y=f(x), прави x = a и x = b и сегмент от оста вол.

Неправилни интеграли

Интеграли с безкрайни граници и интеграли на прекъснати (неограничени) функции се наричат не твоя собствена. Неправилни интеграли от първи род -това са интеграли върху безкраен интервал, дефиниран както следва:

(8.7)

Ако тази граница съществува и е крайна, тогава тя се нарича конвергентен неправилен интеграл от f(x)на интервала [a,+ ∞), и се извиква функцията f(x). интегрируеми в безкраен интервал[a,+ ∞). В противен случай се казва, че интегралът е не съществува или се разминава.

Неправилните интеграли на интервалите (-∞,b] и (-∞, + ∞) се дефинират по подобен начин:

Нека дефинираме понятието интеграл на неограничена функция. Ако f(x) е непрекъснато за всички стойности хсегмент , с изключение на точката c, в която f(x) има безкраен прекъсване, тогава неправилен интеграл от втори вид f(x) вариращи от a до bсумата се нарича:

ако тези граници съществуват и са крайни. Обозначаване:

Примери за интегрални изчисления

Пример 3.30.Изчислете ∫dx/(x+2).

Решение.Нека означим t = x+2, тогава dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Пример 3.31. Намерете ∫ tgxdx.

Решение.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Нека t=cosx, тогава ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Пример3.32 . Намерете ∫dx/sinx

Решение.

Пример3.33. Намирам .

Решение. = .

Пример3.34 . Намерете ∫arctgxdx.

Решение. Нека интегрираме по части. Нека означим u=arctgx, dv=dx. Тогава du = dx/(x 2 +1), v=x, откъдето ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; защото
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример3.35 . Изчислете ∫lnxdx.

Решение.Прилагайки формулата за интегриране по части, получаваме:
u=lnx, dv=dx, du=1/x dx, v=x. Тогава ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Пример3.36 . Изчислете ∫e x sinxdx.

Решение.Нека означим u = e x, dv = sinxdx, тогава du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Също така интегрираме интеграла ∫e x cosxdx по части: u = e x, dv = cosxdx, du=e x dx, v=sinx. Ние имаме:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получихме отношението ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, от което 2∫e x sinx dx = - e x cosx + e x sinx + C.

Пример 3.37. Изчислете J = ∫cos(lnx)dx/x.

Решение.Тъй като dx/x = dlnx, тогава J= ∫cos(lnx)d(lnx). Заменяйки lnx с t, стигаме до интеграла на таблицата J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Изчислете J = .

Решение.Като се има предвид, че = d(lnx), заместваме lnx = t. Тогава J = .

Пример 3.39 . Изчислете интеграла J = .

Решение.Ние имаме: . Следователно =
=
=. въведено по този начин: sqrt(tan(x/2)).

И ако в прозореца с резултати щракнете върху Покажи стъпки в горния десен ъгъл, ще получите подробно решение.